Lecture 19 (5/9/2022)¶
Announcements
Last time we covered:
Evaluating classification algorithms
Today’s agenda:
Evaluating classification algorithms cont’d (ROC curves)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
Advanced classifier evaluation: ROC curves¶
First, let’s load in the iris dataset and remind ourselves what it is we’re classifying to begin with…
iris = sns.load_dataset('iris')
iris
sns.scatterplot(data = iris, x = "sepal_length", y = "sepal_width", hue = "species", alpha = 0.5)
plt.show()
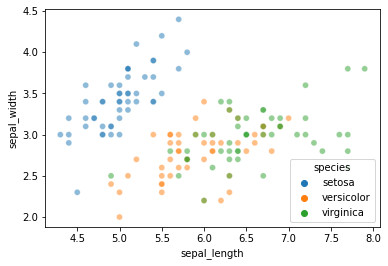
Last time, we discussed:
How to fit a \(k\)-nearest neighbors (k-NN) classification model to this data
How to evaluate its performance on held-out or cross-validated test data
Let’s quickly review this together by having you code and run the steps above yourself!
# Let's start by changing this to a binary classification problem
iris['species_binary'] = iris['species'].map({'versicolor': 'versicolor',
'virginica': 'non-versicolor',
'setosa': 'non-versicolor'})
### YOUR CODE HERE
# 1. Select the `sepal_length` and `sepal_width` columns as X values
# 2. Select the `species_binary` column we generated above as y values
# 3. Use the `train-test-split` function to generate a set of training and test data points
# Use 0.2 for the test portion and set `random_state = 0` to make our results identical
# Don't forget to call `reset_index(drop = True)` for each of your train/test datasets
### YOUR CODE HERE
# 4. Fit an sklearn `KNeighborsClassifier` instance to this data with 3 neighbors
# 5. Evaluate the classifier using accuracy as a baseline metric
# 6. Evaluate the classifier with a more sophisticated metric like F1 score
Hard and Soft Classification¶
The \(k\)-nearest neighbors classifier chooses a predicted label \(\hat{\lambda}\) for a new set of features \(\theta\) by selecting the mode of the labels of the nearest training items.
In this way, you can think of the nearest neighbors as essentially “voting” for the label of each test item. This produces a single label prediction for each test item. Put another way, all the predictions for our test items in the example above are either 'versicolor' or 'non-versicolor'. This sort of model decision policy is referred to as Hard Classification.
But, it doesn’t need to be this way. We can also represent the “votes” of the nearest neighbors as generating a probability distribution over \(\hat{\lambda}\) values.
For example, if there are 3 nearest neighbors for our new item and 2 are ‘versicolor’ and 1 is ‘non-versicolor’, we can represent the new item as having a 2/3 chance of being ‘versicolor’.
Many of the classification algorithms we’ll discuss can assign a probability of a particular label for a given test item rather than a strict label assignment.
This form of classification is called Soft Classification.
The sklearn KNeighborsClassifier class exports a predict_proba function that is just like the predict function except instead of showing us the hard predictions for each test item, it shows us the soft prediction probabilities:
# Here's the original `predict` function
knn.predict(X = xtest)
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
<ipython-input-6-baf57049ea54> in <module>
1 # Here's the original `predict` function
----> 2 knn.predict(X = xtest)
3
NameError: name 'knn' is not defined
# Here's the graded probability prediction
knn.predict_proba(X = xtest)
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
<ipython-input-7-9b573d794d94> in <module>
1 # Here's the graded probability prediction
----> 2 knn.predict_proba(X = xtest)
3
NameError: name 'knn' is not defined
In the predictions above, the first column is the probability of ‘non-versicolor’ and the second is the probability of ‘versicolor’.
This Soft Classification allows us to set more flexible decision policies about what kind of label \(\hat{\lambda}\) we want to assign to a given test item. Using the mode of the nearest neighbor labels in k-NN classification sets a classification threshold of 50% (for binary classification), but we could choose any threshold we want depending on the problem.
In some cases, we may want to predict a label value whenever any of the neighbors have that label (ex. risk of a fatal disease).
Or, maybe we only want to predict a particular label if 90% of the neighbors have that label (ex. setting a high parole).
However, the classification threshold we set will effect how often we assign a particular label to new pieces of data.
Why does this matter?
Different thresholds change evaluation metrics¶
Critically, our choice of classification threshold will affect our evaluation metrics above in predictable ways.
In our iris dataset, labeling new data points based on the mode of 3 nearest neighbors sets a threshold of 2/3 for ‘versicolor’ labels.
If we set a lower threshold of 1/3:
We will label more test items as ‘versicolor’ since we only need 1 out of 3 neighbors to be ‘versicolor’
We will have a higher true positive rate (and lower false negative rate) because we are more likely to detect all true versicolor items this way
But, we will have a higher false positive rate (and lower true negative rate) since we will label more things as ‘versicolor’ that shouldn’t be due to our low threshold.
If instead we set a very high threshold of 3/3:
We will label fewer test items as ‘versicolor’ since we now need 3 out of 3 neighbors to be ‘versicolor’ before labeling a new item ‘versicolor’.
We will have a lower true positive rate (and higher false negative rate) because we are more likely to pass up on some true versicolor items this way
We will have a lower false positive rate (and higher true negative rate) since we will label few things as ‘versicolor’ that shouldn’t be due to our high threshold.
Let’s illustrate this by looking at this pattern in our data.
ROC curves: expressing accuracy across different thresholds¶
Below, we’re going to compute the “versicolor probability” in our test set from above for a classifier with 5 nearest neighbors.
Then, we’ll look at how different thresholds for identifying test items as ‘versicolor’ change our true positive rate and false positive rate in opposite directions.
Step 1: use the k-NN predict_proba function shown above to get probability values for each test item \(p(\text{'versicolor'})\) rather than hard classifications
knn = KNeighborsClassifier(n_neighbors = 5).fit(X = xtrain, y = ytrain)
# Here's our soft classification with 5 nearest neighbors (converted to dataframe for easier processing)
versicolor_probs = pd.DataFrame(knn.predict_proba(X = xtest),
columns = ["non-versicolor_prob", "versicolor_prob"]
)
# Let's add the true values for comparison
versicolor_probs['true_label'] = ytest
versicolor_probs
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
<ipython-input-8-a2bc349bf354> in <module>
----> 1 knn = KNeighborsClassifier(n_neighbors = 5).fit(X = xtrain, y = ytrain)
2
3 # Here's our soft classification with 5 nearest neighbors (converted to dataframe for easier processing)
4 versicolor_probs = pd.DataFrame(knn.predict_proba(X = xtest),
5 columns = ["non-versicolor_prob", "versicolor_prob"]
NameError: name 'KNeighborsClassifier' is not defined
Step 2: Now, let’s pick a range of classification thresholds for ‘versicolor’ and show how this changes what values we assign to the test items.
For \(k\)-nearest neighbors, the thresholds are intuitive because we can break them out by each possible voting arrangement of our 5 neighbors.
# Which test items get labeled 'versicolor' if you only need 1 nearest neighbor to be versicolor?
versicolor_probs['k1_label'] = np.where( # np.where is like an "if-else" condition for this column value
versicolor_probs['versicolor_prob'] >= 0.2, # condition
'versicolor', # value in all rows where condition above is True
'non-versicolor' # value in all rows where condition above is False
)
# Which test items get labeled 'versicolor' if you need at least 2 nearest neighbors to be versicolor?
versicolor_probs['k2_label'] = np.where(
versicolor_probs['versicolor_prob'] >= 0.4,
'versicolor',
'non-versicolor'
)
# Which test items get labeled 'versicolor' if you need at least 3 nearest neighbors to be versicolor?
versicolor_probs['k3_label'] = np.where(
versicolor_probs['versicolor_prob'] >= 0.6,
'versicolor',
'non-versicolor'
)
# Which test items get labeled 'versicolor' if you need at least 4 nearest neighbors to be versicolor?
versicolor_probs['k4_label'] = np.where(
versicolor_probs['versicolor_prob'] >= 0.8,
'versicolor',
'non-versicolor'
)
# Which test items get labeled 'versicolor' if you need *all 5* nearest neighbors to be versicolor?
versicolor_probs['k5_label'] = np.where(
versicolor_probs['versicolor_prob'] >= 1.0,
'versicolor',
'non-versicolor'
)
versicolor_probs
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
<ipython-input-9-3daa2b3a961e> in <module>
1 # Which test items get labeled 'versicolor' if you only need 1 nearest neighbor to be versicolor?
2 versicolor_probs['k1_label'] = np.where( # np.where is like an "if-else" condition for this column value
----> 3 versicolor_probs['versicolor_prob'] >= 0.2, # condition
4 'versicolor', # value in all rows where condition above is True
5 'non-versicolor' # value in all rows where condition above is False
NameError: name 'versicolor_probs' is not defined
Step 3: How do our true positive rate and false positive rate change for each of these thresholds?
from sklearn.metrics import recall_score
# What's the TPR for our lowest threshold (k1) above?
k1_tpr = recall_score(y_true = versicolor_probs['true_label'],
y_pred = versicolor_probs['k1_label'],
labels = ['versicolor', 'non-versicolor'],
pos_label = 'versicolor'
)
# What's the FPR for our lowest threshold (k1) above?
# Note FPR = 1 - TNR and TNR is just the recall (TPR) for the *negative* label, which we can set below
k1_fpr = 1 - recall_score(y_true = versicolor_probs['true_label'],
y_pred = versicolor_probs['k1_label'],
labels = ['versicolor', 'non-versicolor'],
pos_label = 'non-versicolor' # positive label
)
# Same as above for k2 threshold
k2_tpr = recall_score(y_true = versicolor_probs['true_label'],
y_pred = versicolor_probs['k2_label'],
labels = ['versicolor', 'non-versicolor'],
pos_label = 'versicolor'
)
k2_fpr = 1 - recall_score(y_true = versicolor_probs['true_label'],
y_pred = versicolor_probs['k2_label'],
labels = ['versicolor', 'non-versicolor'],
pos_label = 'non-versicolor'
)
# Same as above for k3 threshold
k3_tpr = recall_score(y_true = versicolor_probs['true_label'],
y_pred = versicolor_probs['k3_label'],
labels = ['versicolor', 'non-versicolor'],
pos_label = 'versicolor'
)
k3_fpr = 1 - recall_score(y_true = versicolor_probs['true_label'],
y_pred = versicolor_probs['k3_label'],
labels = ['versicolor', 'non-versicolor'],
pos_label = 'non-versicolor'
)
# Same as above for k4 threshold
k4_tpr = recall_score(y_true = versicolor_probs['true_label'],
y_pred = versicolor_probs['k4_label'],
labels = ['versicolor', 'non-versicolor'],
pos_label = 'versicolor'
)
k4_fpr = 1 - recall_score(y_true = versicolor_probs['true_label'],
y_pred = versicolor_probs['k4_label'],
labels = ['versicolor', 'non-versicolor'],
pos_label = 'non-versicolor'
)
# Same as above for k5 threshold
k5_tpr = recall_score(y_true = versicolor_probs['true_label'],
y_pred = versicolor_probs['k5_label'],
labels = ['versicolor', 'non-versicolor'],
pos_label = 'versicolor'
)
k5_fpr = 1 - recall_score(y_true = versicolor_probs['true_label'],
y_pred = versicolor_probs['k5_label'],
labels = ['versicolor', 'non-versicolor'],
pos_label = 'non-versicolor'
)
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
<ipython-input-10-2700b5f571a0> in <module>
2
3 # What's the TPR for our lowest threshold (k1) above?
----> 4 k1_tpr = recall_score(y_true = versicolor_probs['true_label'],
5 y_pred = versicolor_probs['k1_label'],
6 labels = ['versicolor', 'non-versicolor'],
NameError: name 'versicolor_probs' is not defined
Phew! Now let’s combine the above to see how they compare:
# For each of our thresholds, what is the true positive rate and the false positive rate?
np.arange(0, 1.1, 0.2)
roc_df = pd.DataFrame({
"threshold": np.arange(0.2, 1.1, 0.2),
"TPR": [k1_tpr, k2_tpr, k3_tpr, k4_tpr, k5_tpr],
"FPR": [k1_fpr, k2_fpr, k3_fpr, k4_fpr, k5_fpr]
})
roc_df
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
<ipython-input-11-9c9e8e96c008> in <module>
4 roc_df = pd.DataFrame({
5 "threshold": np.arange(0.2, 1.1, 0.2),
----> 6 "TPR": [k1_tpr, k2_tpr, k3_tpr, k4_tpr, k5_tpr],
7 "FPR": [k1_fpr, k2_fpr, k3_fpr, k4_fpr, k5_fpr]
8 })
NameError: name 'k1_tpr' is not defined
Now, our final step is to graph this relationship.
This is called an ROC curve (Receiver Operating Characteristic) and we’ll see why it’s useful once we’ve plotted it.
# ROC curve by hand
g = sns.pointplot(
data = roc_df,
x = "FPR",
y = "TPR"
)
g.set_xlabel("False Positive Rate")
g.set_ylabel("True Positive Rate")
g.set_xticklabels([])
g.set_yticklabels([])
plt.show()
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
<ipython-input-12-6debca9fd19b> in <module>
2
3 g = sns.pointplot(
----> 4 data = roc_df,
5 x = "FPR",
6 y = "TPR"
NameError: name 'roc_df' is not defined
What is that??
Answer: a somewhat clumsy ROC curve (since we’re not working with much data here).
What does this mean?
Each of our points above is the TPR and FPR for a given classification threshold
When we set a low threshold, we expect TPR and FPR to be very high (top right)
When we set a high threshold, we expect TPR and FPR to both be very low (bottom left)
What about in between?
For every threshold in between the top right (low) and bottom left (high), we want to keep TPR high while FPR goes down.
Put another way, we want to reduce FPR without having to also sacrifice TPR.
Given the above, a good ROC curve is one that swings as close to the top left portion of the axes as possible.
Here’s a picture that illustrates this:
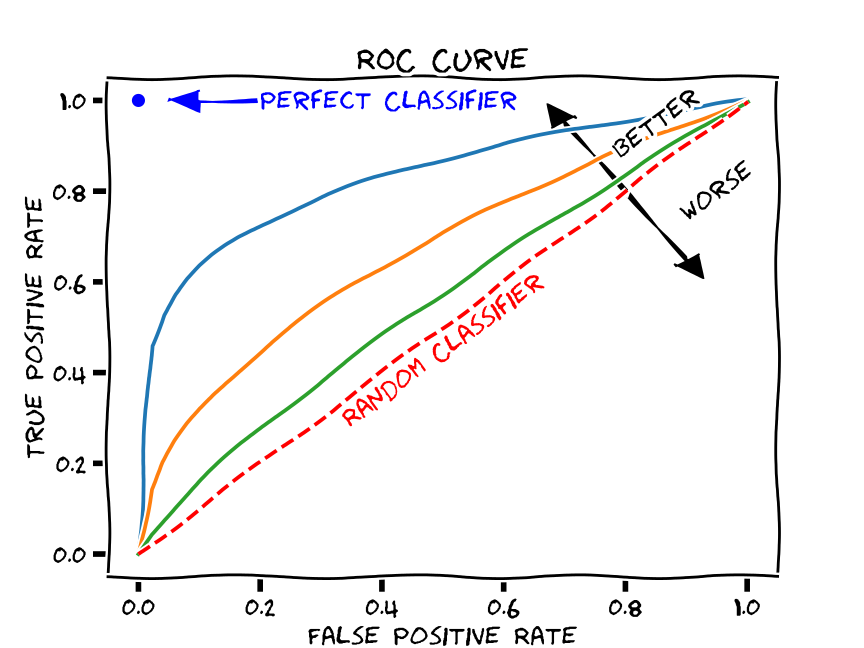
(source)
Compared to what?
Note the dashed line across the middle. This indicates what you would expect to happen with TPR and FPR if your classifier was random. In other words, we can compare our ROC curve to the “random classifier” line to determine how much better our classifier is doing than random guessing.
We use a metric called area under the curve (AUC) to calculate this difference.
This measures the area under the ROC curve. The value ranges from 0 to 1, but since a random classifier has an AUC of 0.5, we’re looking for values > 0.5.
ROC curves in scikit-learn¶
Fortunately, we don’t need to do all the manual calculations above to generate an ROC curve.
As usual, scikit-learn has us covered!
Below, we call the roc_curve function to generate an ROC curve:
from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(
y_true = ytest,
y_score = knn.predict_proba(X = xtest)[:, 1],
pos_label = 'versicolor'
)
tpr
fpr
thresholds
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
<ipython-input-13-2e3941cb1b54> in <module>
2
3 fpr, tpr, thresholds = roc_curve(
----> 4 y_true = ytest,
5 y_score = knn.predict_proba(X = xtest)[:, 1],
6 pos_label = 'versicolor'
NameError: name 'ytest' is not defined
Then, we can graph the results:
g = sns.pointplot(
x = fpr,
y = tpr
)
g.set_xlabel("False Positive Rate")
g.set_ylabel("True Positive Rate")
g.set_xticklabels(np.arange(0, 1.1, 0.2))
plt.show()
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
<ipython-input-14-cfb6b5f8de64> in <module>
1 g = sns.pointplot(
----> 2 x = fpr,
3 y = tpr
4 )
5
NameError: name 'fpr' is not defined
AUC¶
scikit-learn also exports an AUC function that will report how our ROC curve fares:
from sklearn.metrics import roc_auc_score
roc_auc_score(
y_true = ytest,
y_score = knn.predict_proba(X = xtest)[:, 1], # get probabilities for 'versicolor'
labels = ['versicolor', 'non-versicolor']
)
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
<ipython-input-15-ffbfe1299508> in <module>
3
4 roc_auc_score(
----> 5 y_true = ytest,
6 y_score = knn.predict_proba(X = xtest)[:, 1], # get probabilities for 'versicolor'
7 labels = ['versicolor', 'non-versicolor']
NameError: name 'ytest' is not defined
Evaluating classification algorithms: summary¶
When we use a classification algorithm like \(k\)-nearest neighbors, we want a way to quantify how well it performs with test data.
The most intuitive way to do so is with accuracy, but this can mis-construe our classifier’s performance when we have imbalanced data.
Alternatives that rely on the confusion matrix allow us to weight the relative impact of different kinds of errors (false positives and false negatives).
Recognizing that our rate of false positives and false negatives is sensitive to the classification threshold used in our model (e.g., the “voting” procedure in k-NN), we can use an ROC curve to examine the classifier’s success across a range of thresholds.
